EM-NN-GAMP: Recovering Linearly-Constrained Non-Negative Sparse Signals

Overview

The Expectation-Maximization Non-negative Approximate Message Passing (EM-NN-GAMP) is a collection of empirical-Bayes algorithms designed to recover a sparse signal \( \boldsymbol{x} \in \mathbb{R}^N\) from (possibly) noisy measurements \( \boldsymbol{y} = \boldsymbol{Ax} + \boldsymbol{w}\). We focus on non-negative (NN) signals (i.e., \( x_n \geq 0 \ \forall n\)) that obey the linear equality constraints \( \boldsymbol{Bx} = \boldsymbol{c} \in \mathbb{R}^P\). A notable example is the simplex constraint (i.e., the signal is NN and sums to one), occuring in hyperspectral image unmixing, portfolio optimization, density estimation, and other examples.

One approach to recovering the constrained sparse signal is to solve the convex optimization problem \[ \hat{\boldsymbol{x}} = \arg\min_{\boldsymbol{x} \geq \boldsymbol{0}} \tfrac{1}{2}\| \boldsymbol{y} - \boldsymbol{Ax}\|_2^2 + \lambda \| \boldsymbol{x}\|_1 \text{ s.t. } \boldsymbol{Bx} = \boldsymbol{c}.\] Our first algorithm, NN Least-Squares AMP (NNLS-GAMP), solves the above problem with \( \lambda = 0 \) using the max-sum version of the generalized approximate message passing (GAMP) algorithm.

Our second algorithm, expectation maximization NN LASSO AMP (EM-NNL-GAMP) solves the above problem using the max-sum version of GAMP. Moreover, we use the expectation maximization (EM) algorithm to automatically tune the penalty parameter \( \lambda \geq 0\) while estimating the signal.

Our third algorithm, EM NN Gaussian-Mixture AMP (EM-NNGM-GAMP), aims to solve not an optimization problem (like above) but rather an inference problem: compute the MMSE estimate of a linearly constrained NN sparse signal from noisy linear observations. To do so, we place an i.i.d. Bernoulli NN Gaussian mixture prior on the signal and use the sum-product version of GAMP to recover the signal while tuning the NNGM's parameters using EM.

To enforce the linear equality constraints with NNLS-GAMP, EM-NNL-GAMP, or EM-NNGM-GAMP, we augment the observation model to \[ \begin{bmatrix} \boldsymbol{y} \\ \boldsymbol{c} \end{bmatrix} = \begin{bmatrix} \boldsymbol{A} \\ \boldsymbol{B} \end{bmatrix} \boldsymbol{x} + \begin{bmatrix} \boldsymbol{w} \\ \boldsymbol{0}\end{bmatrix}\] and place a Dirac delta likelihood on the appended measurements. Additionally, we develop an additive white Laplacian noise model that assumes the absolute loss \( \| \boldsymbol{y} - \boldsymbol{Ax}\|_1\) for improved robustness of outliers.

Advantages of EM-NN-GAMP

We highlight some of EM-NN-GAMP's advantages below:

  1. EM-NNL-GAMP removes the need to hand tune Bx = c for the NN LASSO problem.
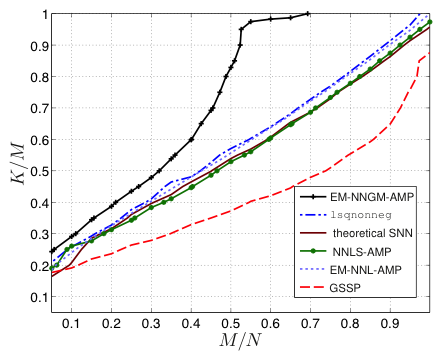
  2. State-of-the-art noiseless phase transitions of simplex-obeying sparse Dirichlet signals using EM-NNGM-GAMP.
  3. State-of-the-art noisy recovery of a NN image for all undersampling ratios using EM-NNGM-GAMP.
  4. Excellent performance on the portfolio optimization problem using the return-adjusted Markowitz mean-variance framework. When coupled with the additive white Laplacian noise model, performance improves further.
  5. Very good complexity scaling with problem dimensions and can leverage fast operators such as FFTs.

Matlab code

The EM-NN-GAMP MATLAB function attempts to recover a signal through measurements observed from the above linear model using any of the three algorithms. In addition, EM-NN-GAMP has some optional inputs to improve computation time/accuracy, along with toggles for learning of the prior's parameters. The algorithm's usage can be seen in the Examples section.

Authors

Please contact the following authors regarding any questions:

Publications

The details are in:

Journal

  1. J. Vila and P. Schniter, ``An Empirical-Bayes Approach to Recovering Linearly Constrained Non-Negative Sparse Signals [pdf] [arxiv],'' IEEE Transactions on Signal Processing, vol. 62, no. 18, pp. 4689-4703, Sep. 2014.

Conference

  1. J. Vila and P. Schniter, ``An Empirical-Bayes Approach to Recovering Linearly Constrained Non-Negative Sparse Signals [pdf],'' Proc. IEEE Intl. Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP) (Saint Martin Island), Dec. 2013.

Support

This work has been supported in part by NSF grants IIP-0968910, CCF- 1018368, CCF-1218754, and by DARPA/ONR grant N66001-10-1-4090

know pasting counter
Visits Stats

© 2015 Jeremy Vila
Template design by Andreas Viklund