EM-GM-GAMP

EM-GM-GAMP: An Algorithm for Sparse Reconstruction

Overview

The Expectation-Maximization Gaussian-Mixture Approximate Message Passing (EM-GM-GAMP) is an algorithm designed to recover a signal \( \boldsymbol{x} \in \mathbb{R}^N\) from (possibly) noisy measurements \( \boldsymbol{y} = \boldsymbol{Ax} + \boldsymbol{w} \in \mathbb{R}^M \). One particularly interesting case is when the measurements are undersampled (i.e. \( M \lt N\)). With sufficient signal sparsity and a well-conditioned mixing matrix, signal recovery is possible.

EM-GM-GAMP assumes a sparsity promoting i.i.d. Gaussian-Mixture prior: \( p(x_n) = \lambda \sum_{\ell = 1}^L \omega_\ell \mathcal{N}(x_n; \theta_\ell, \phi_\ell) + (1 - \lambda) \delta(x_n)\) , and i.i.d. additive Gaussian noise prior:\( p(w_m) = \mathcal{N}(w_m;0, \psi) \) . It then uses the Generalized Approximate Message Passing (GAMP) algorithm to evaluate the means (MMSE estimates) and variances of the posterior \( p(\boldsymbol{x}|\boldsymbol{y})\). After running GM-AMP, we then find the Expectation-Maximization (EM) updates of the parameters \( \boldsymbol{q} \triangleq [\lambda, \boldsymbol{\omega}, \boldsymbol{\theta}, \boldsymbol{\phi} ,\psi]\) and repeat GM-AMP until convergence. (See publications below for details.)

The EM-GM-GAMP MATLAB function attempts to recover a signal through measurements observed from the above linear model. In addition, EM-GM-GAMP has some optional inputs to improve computation time/accuracy. EM-GM-GAMP now supports the MMV model as well as both real and complex signals. Examples of the function's usage can be seen in the Examples section.

EM-GM-GAMP is a more "flexible" version of EM-Bernoulli-Gaussian AMP. It allows for the GM prior to learn a broader class of signal priors, such as the Bernoulli-Rademacher signals. In this fashion, we aim to leverage the empirical pdf of an arbitrary signal to aid in its recovery.

Advantages of EM-GM-GAMP

We highlight some of EM-GM-GAMP's advantages below:

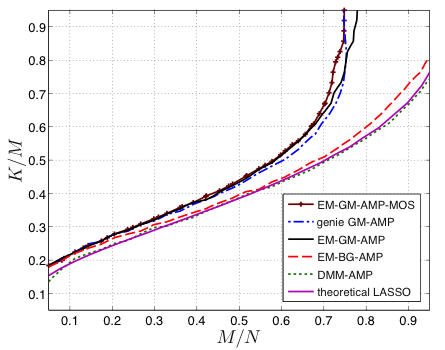
State-of-the-art noiseless recovery performance over a wide range of signal types.
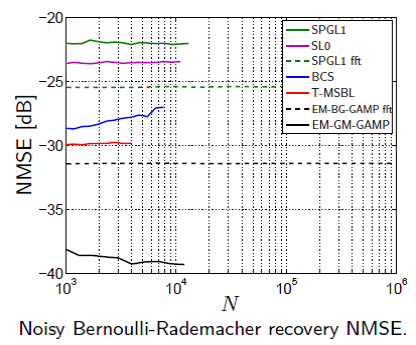
State-of-the-art noisy recovery NMSE over a wide range of signal types.
Numerical Experiments demonstrate this performance over a range of SNRs.
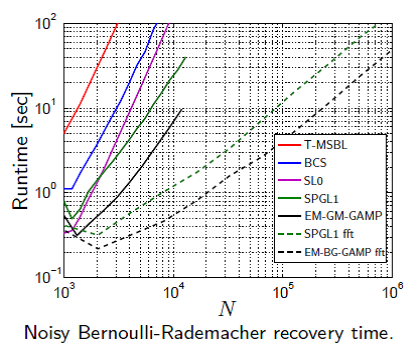
Very good complexity scaling with problem dimensions

Authors

Please contact the following authors regarding any questions:

Jeremy Vila (OSU) - Email: vilaj@ece.osu.edu
Phil Schniter (OSU) - Email: schniter@ece.osu.edu

Publications

The details are in:

Journal

J. P. Vila and P. Schniter, ``Expectation-Maximization Gaussian-Mixture Approximate Message Passing [pdf][arxiv],'' IEEE Transactions on Signal Processing, vol. 61, no. 19, pp. 4658-4672, Oct. 2013.

Conference

J. P. Vila and P. Schniter, ``Expectation-Maximization Gaussian-Mixture Approximate Message Passing [pdf],'' Proc. Conf. on Information Sciences and Systems, (Princeton, NJ), Mar. 2012. (Invited.) [slides]

Poster

J. P. Vila and P. Schniter, ``An Empirical-Bayes Approach to Compressive Sensing via Approximate Message Passing [pdf],'' presented at the Duke Workshop on Sensing and Analysis of High-Dimensional Data (SAHD) (Durham, North Carolina), July 2011. [poster]

Support

This work has been supported in part by NSF-I/UCRC grant IIP-0968910, by NSF grant CCF-1018368, and by DARPA/ONR grant N66001-10-1-4090.

Web Counter