EM-BG-GAMP: An Algorithm for Sparse Reconstruction
Overview
The Expectation-Maximization Bernoulli-Gaussian Approximate Message Passing (EM-BG-GAMP) is an algorithm designed to recover a signal \( \boldsymbol{x} \in \mathbb{R}^N \) from (possibly) noisy measurements \( \boldsymbol{y} = \boldsymbol{Ax} + \boldsymbol{w} \in \mathbb{R}^M\) . One particularly interesting case is when the measurements are undersampled (i.e. \( M \lt N \)). With sufficient signal sparsity and a well-conditioned mixing matrix, signal recovery is possible.
EM-BG-GAMP assumes a sparsity promoting i.i.d. Bernoulli-Gaussian prior: \( p(x_n) = (1-\lambda)\delta(x_n) + \lambda \mathcal{N}(x_n; \theta,\phi) \) and i.i.d. additive Gaussian noise: \( p(w_m) = \mathcal{N}(w_m;0,\psi)\) . It then uses the Generalized Approximate Message Passing (GAMP) algorithm to evaluate the means (MMSE estimates) and variances of the posterior \(p(\boldsymbol{x}|\boldsymbol{y}) \). After running BG-GAMP, we then find the Expectation-Maximization (EM) updates of the parameters \( \boldsymbol{q} \triangleq [\lambda, \theta, \phi, \psi]\) and repeat BG-GAMP until convergence. (See publications below for details.)
The EM-BG-GAMP MATLAB function attempts to recover a signal through measurements observed from the above linear model. Unlike some other compressive sensing algorithms (i.e. LASSO), EM-BG-GAMP does not require any tuning parameters. EM-BG-GAMP does, however, have some optional inputs to improve computation time/accuracy. Currently, EM-BG-GAMP supports both real and complex signals. Examples of the function's usage can be seen in the Examples section.
Advantages of EM-BG-GAMP
There are plenty of compressive-sensing algorithms available. Why use EM-BG-GAMP? Here are a few advantages of our approach.
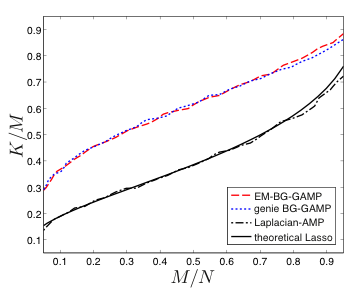
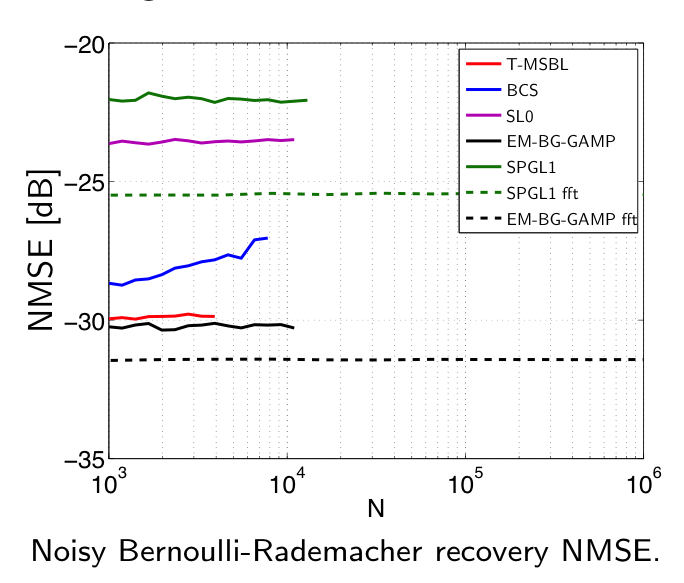
- Excellent recovery performance over a wide range of signal/matrix types.
- Very good complexity scaling with problem dimensions
- No required tuning parameters.

Authors
Please contact the following authors regarding any questions:
- Jeremy Vila (OSU) - Email: vilaj@ece.osu.edu
- Phil Schniter (OSU) - Email: schniter@ece.osu.edu
Publications
The details are in:
Journal
- J. P. Vila and P. Schniter, ``Expectation-Maximization Gaussian-Mixture Approximate Message Passing [pdf][arxiv],'' IEEE Transactions on Signal Processing, vol. 61, no. 19, pp. 4658-4672, Oct. 2013.
Conference
- J. P. Vila and P. Schniter, ``Expectation-Maximization Bernoulli-Gaussian Approximate Message Passing [pdf],'' Proc. Asilomar Conf. on Signals, Systems, and Computers (Pacific Grove, CA), Nov. 2011. [slides]
Poster
- J. P. Vila and P. Schniter, ``An Empirical-Bayes Approach to Compressive Sensing via Approximate Message Passing [pdf],'' presented at the Duke Workshop on Sensing and Analysis of High-Dimensional Data (SAHD) (Durham, North Carolina), July 2011. [poster]
Support
This work has been supported in part by NSF-I/UCRC grant IIP-0968910, by NSF grant CCF-1018368, and by DARPA/ONR grant N66001-10-1-4090.
Visit Counter
© 2011 Jeremy Vila
Template design by Andreas Viklund