News
Our BiG-AMP manuscript (see arXiv version) has been accepted as a two-part paper by the IEEE Transactions on Signal Processing. The paper includes a detailed derivation of the algorithm, an adaptive damping mechanism that aids convergence under finite problem sizes, an expectation-maximization (EM)-based method to automatically tune the parameters of the assumed priors, two rank-selection strategies, and an extensive empirical study comparing BiG-AMP to state of the art algorithms for matrix completion, robust PCA, and dictionary learning.
BiG-AMP is now available for download as part of the GAMPMATLAB package. See the Download page to obtain the code.
Overview
Bilinear Generalized Approximate Message Pasing (BiG-AMP) extends the Generalized AMP framework, originally proposed for high-dimensional generalized-linear regression in the context of compressive sensing, to the generalized-bilinear case, which enables its application to matrix completion, robust PCA, dictionary learning, and related matrix-factorization problems.
Signal Model
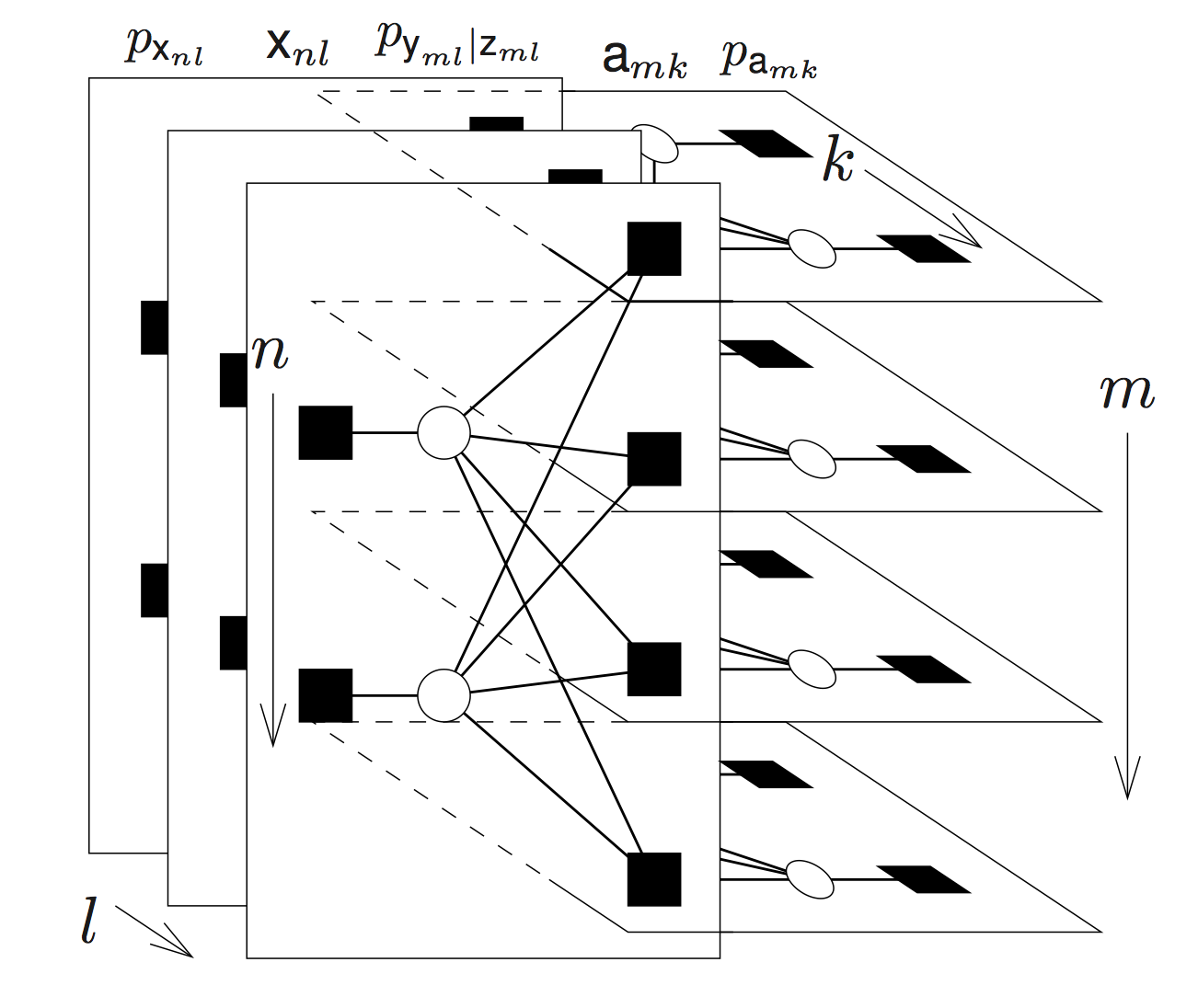
In particular, BiG-AMP is an algorithmic framework for the following generalized bilinear inference problem: estimate the matrices \(\boldsymbol{A} = [a_{mn}] \in \mathbb{R}^{M \times N}\) and \(\boldsymbol{X} = [x_{nl}] \in \mathbb{R}^{N \times L}\) from a matrix observation \(\boldsymbol{Y}\in\mathbb{R}^{M \times N}\) that is statistically coupled to their product, \(\boldsymbol{Z} \triangleq\boldsymbol{A} \boldsymbol{X}\). In doing so, we treat \(\boldsymbol{A}\) and \(\boldsymbol{X}\) as realizations of random matrices \(\mathbf{\mathsf{A}}\) and \(\mathbf{\mathsf{X}}\) with known separable pdfs (or pmfs in the case of discrete models), i.e., \[ p_{\mathbf{\mathsf{A}}}(\boldsymbol{A}) = \prod_m \prod_n p_{\mathbf{\mathsf{a}}_{mn}}(a_{mn})\\ p_{\mathbf{\mathsf{X}}}(\boldsymbol{X}) = \prod_n \prod_l p_{\mathbf{\mathsf{x}}_{nl}}(x_{nl})\\ \] and we likewise assume that the likelihood function of \(\boldsymbol{Z}\) is known and separable, i.e., \[ p_{\mathbf{\mathsf{Y}}|\mathbf{\mathsf{Z}}}(\boldsymbol{Y}|\boldsymbol{Z}) = \prod_m \prod_l p_{\mathbf{\mathsf{y}}_{ml}|\mathbf{\mathsf{z}}_{ml}}({y}_{ml}|{z}_{ml}). \] With appropriate choices for these priors, BiG-AMP can be used to solve a wide range of matrix recovery problems with numerous practical applications. See our Publications and Examples for further details.
Features and Advantages
As discussed above, BiG-AMP can be used to solve a variety of matrix recovery problems. Furthermore, EM-BiG-AMP can learn the parameters of the underlying distributions, avoiding the need to tune algorithmic parameters. Our numerical results, using both synthetic and real-world datasets, demonstrate that EM-BiG-AMP yields excellent reconstruction accuracy (often best in class) while maintaining competitive runtimes.
The provided code offers specialized versions of EM-BiG-AMP for matrix completion, dictionary learning, and robust PCA. Mechanisms are also included for adaptive damping to aid convergence for finite problem sizes and to automatically determine the underlying matrix rank. In addition, these codes can easily be extended to other applications by developing new estimator objects within the GAMPMATLAB framework.
Authors
Please contact the authors with questions or comments about BiG-AMP.- Jason T. Parker (AFRL/RYAP) - Email: jason.parker.13@us.af.mil
- Phil Schniter (OSU) - Email: schniter@ece.osu.edu
- Volkan Cevher (EPFL) - Email: volkan.cevher@epfl.ch
Support
Support for this project was provided by an AFOSR lab task under the direction of Dr. Arje Nachman. Support was also provided by NSF grants IIP-0968910, CCF-1018368, CCF-1218754, and by DARPA/ONR grant N66001-10-1-4090
© 2013 Jason T. Parker
Template design by Andreas Viklund